本文將繼續根據最新的考研大綱，繼續梳理高等數學在數學（一）、數學（二）、數學（三）的公共部分。在這里，對于數學（一）和數學（二）單獨考點，包新卓老師會在相應的內容后面予以標出，未做任何標出的內容則為數學（一）、數學（二）、數學（三）的公共考點。

六、常微分方程

常微分方程是與微積分有緊密聯系的一門數學分支、在實際問題中有重要應用。利用常微分方程建立實際問題的數學模型和方程的求解是這部分內容的兩個核心問題。

考綱內容：

1、常微分方程的基本概念：了解微分方程及其階、解、通解、初始條件和特解等概念；

2、變量可分離的微分方程、、齊次微分方程、一階線性微分方程：掌握變量可分離的微分方程及一階線性微分方程的解法，會解齊次微分方程；

3、（數一）伯努利方程、全微分方程、可用簡單的變量代換求解某些微分方程：會解伯努利和全微分方程，會用簡單的變量代換求解某些微分方程；

4、（數一、數二）可降階的高階微分方程：會用降階法解下列形式的微分方程：

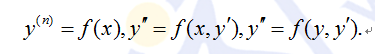
5、線性微分方程解的性質及解的結構定理：理解線性微分方程解的性質及解的結構；

6、二階常系數齊次線性微分方程：掌握二階常系數齊次線性微分方程的解法；

7、（數一、數二）高于二階的某些常系數齊次線性微分方程：會求解某些高于二階的某些常系數齊次線性微分方程；

8、簡單的二階常系數非齊次線性微分方程：會解自由項為多項式、指數函數、正弦函數、余弦函數，（數一、數二）以及這些自由項的和與積的二階常系數非齊次線性微分方程；

9、（數一）歐拉方程：會解歐拉方程；

10、微分方程的簡單應用：會用微分方程解決一些簡單的應用問題，（數三）會用微分方程求解簡單的經濟應用問題。

七、差分方程（數三）

考綱內容：

1、差分與差分方程的概念、差分方程的通解與特解：了解差分與差分方程及其通解與特解等概念；

2、一階常系數線性差分方程：了解一階常系數線性差分方程的求解方法。

八、無窮級數（數一、數三）

1、常數項級數的收斂與發散的概念、收斂級數的和的概念：了解級數的收斂與發散、收斂級數的和的概念；

2、級數的基本性質與收斂的必要條件、幾何級數與p級數及其收斂性、正項級數收斂性的判別法：了解級數的基本性質及級數收斂的必要條件，掌握幾何級數及p級數的收斂與發散的條件，掌握正項級數收斂性的比較判別法和比值判別法；

3、任意項級數的絕對收斂與條件收斂、交錯級數與萊布尼茨定理：了解任意項級數絕對收斂與條件收斂的概念以及絕對收斂與收斂的關系，了解交錯級數的萊布尼茨判別法；

4、冪級數及其收斂半徑、收斂區間（指開區間）和收斂域：理解冪級數收斂半徑的概念，掌握冪級數的收斂半徑、收斂區間及收斂域的求法；

5、冪級數的和函數、冪級數在其收斂區間內的基本性質、簡單冪級數的和函數的求法：掌握冪級數在其收斂區間內的基本性質（和函數的連續性、逐項積分和逐項求導），會求簡單冪級數在其收斂區間內的和函數，并會由此求出某些數項級數的和；

本章節的重點：

1、常數項級數的收斂與發散的概念、基本性質與收斂的必要條件，包新卓老師提醒大家，這些概念是級數的基礎概念，是后續內容的基礎；

2、常用級數的斂散性：幾何級數與p級數；

3、能夠識別數項級數的類型、具備綜合利用性質和主要判別法判斷級數的收斂性的能力；

4、會計算冪級數的收斂半徑、收斂區間、和收斂域，注意收斂區間與收斂域的區別與聯系；

5、注意簡單冪級數的和函數的做法，能夠靈活利用冪級數的分析性質將函數展開成冪級數。

更多精彩資訊請關注查字典資訊網，我們將持續為您更新最新資訊!