| 2017年數三高數 | 2016年數三高數 |
| 考題序號 | 考查知識點 | 解題思路點睛 | 考查知識點 | 解題思路點睛 |
| 1 | 連續的定義 | 一點連續的充要條件,基礎題 | 極值和拐點 | 這種與圖像結合考查的極值和拐點,屬于常考題型,直接利用導數與極值、拐點的關系即可,基礎題 |
| 2 | 多元函數微分學應用(無條件極值) | 按照無條件極值基本步驟計算即可,基礎題 | 偏導數計算 | 偏導數的計算已是基礎題型,只要分別計算一階偏導數驗證選項即可,基礎題 |
| 3 | 導數的應用(單調性) | 通過已知條件加絕對值仍成立,進而推出絕對值函數的符號,得答案,基礎題 | 二重積分比較 | 利用二重積分的性質和輪換對稱性比較即可,基礎題 |
| 4 | 常數項級數的斂散性 | 利用常數項級數收斂判斷即可,基礎題 | 常數項級數的斂散性 | 利用比較判別法判斷是否絕對收斂,也可利用部分和數列判斷斂散性,稍微難一點 |
| 9 | 定積分的特殊計算(對稱區間) | 先利用對稱區間奇偶性化簡定積分,再計算即可,基礎題 | 極限計算 | 利用等價無窮小替換和四則運算,基礎題 |
| 10 | 差分方程 | 帶公式計算即可,基礎題 | 數列極限計算 | 代定積分極限計算公式即可,基礎題 |
| 11 | 導數的經濟學應用 | 帶入基本公式求解,基礎題 | 多元函數的全微分 | 求偏導,代公式,基礎題 |
| 12 | 已知全微分求多元函數 | 利用全微分計算公式,結合不定積分得到f(x,y)的通解,根據f(0,0)=0,得f(x,y)的具體表達式 | 二重積分計算 | 繪圖,利用奇偶對稱性化簡,再計算,注意積分次序的選擇,基礎題 |
| 15 | 含變限積分的極限計算 | 首先對變限積分做還原,利用洛必達法則求解即可,基礎題 | 極限計算 | 冪指函數極限計算,對數恒等變換,利用泰勒公式展開計算,基礎題 |
| 16 | 無界區域的二重積分計算 | 結合積分區域選擇積分次序 | 導數的經濟應用 | 利用彈性公式得到一微分方程,解微分方程,代初解得到需求函數;寫出收益函數,求導計算邊際收益,并給出經濟意義,基礎題 |
| 17 | 定積分定義求極限 | 利用定積分定義化簡極限,最后計算定積分即可,基礎題 | 變限積分求導公式和最值問題 | 根據x,t的大小關系,分段寫出函數,再依題計算計算即可,難度不大,計算稍微大些,易出錯 |
| 18 | 討論方程根的個數 | 建立輔助函數,利用零點定理,推出k的范圍,計算稍大些 | 含變限積分方程的計算 | 先換元求導,得微分方程,求解待初始條件(初始條件隱含在題目中,屬常考題型),基礎題 |
| 19 | 冪級數和微分方程結合出題 | 利用微分方程求解得和函數,難度略大 | 冪級數的收斂域和和函數 | 逐項求導計算,注意步驟,也可先拆分,得到兩個冪函數,再分別計算和函數,進而得到題目所求的和函數,計算量大,易扣步驟分 |
 北京中小學8月29日起分批錯峰開學 2021年1月30日放寒假-查字典資訊網2020-09-15
北京中小學8月29日起分批錯峰開學 2021年1月30日放寒假-查字典資訊網2020-09-15
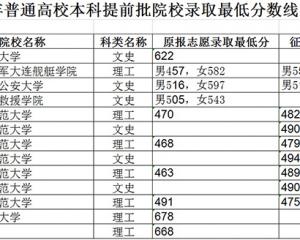 黑龍江:2020年普通高校本科提前批院校錄取最低分數線-查字典資訊網2020-08-19
黑龍江:2020年普通高校本科提前批院校錄取最低分數線-查字典資訊網2020-08-19 交叉學科將成第14個門類,這些高校早已搶占先機!2020-08-10
交叉學科將成第14個門類,這些高校早已搶占先機!2020-08-10 2021考研招生簡章已公布?漢族考生也可享受“少干計劃”的降分優惠?-查字典資訊網2020-08-06
2021考研招生簡章已公布?漢族考生也可享受“少干計劃”的降分優惠?-查字典資訊網2020-08-06