《數學學科知識與教學能力

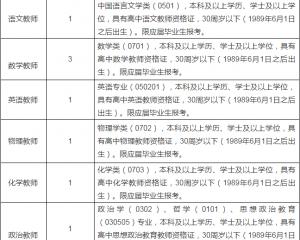
一、考試目標1．數學學科知識的掌握和運用。掌握大學本科數學專業基礎課程的知識和高中數學知識。具有在高中數學教學實踐中綜合而有效地運用這些知識的能力。2．高中數學課程知識的掌握和運用。理解高中數學課程的性質、基本理念和目標，熟悉《普通高中數學課程標準（實驗）

3．教學知識了解包括備課、課堂教學、作業批改與考試、數學課外活動、數學教學評價等基本環節的教學過程。掌握講授法、討論法、自學輔導法、發現法等常見的數學教學方法。掌握概念教學、命題教學等數學教學知識的基本內容。掌握合作學習、探究學習、自主學習等中學數學學習方式。掌握數學教學評價的基本知識和方法。4．教學技能（1）教學設計能夠根據學生已有的知識水平和數學學習經驗，準確把握所教內容與學生已學知識的聯系。能夠根據《課標

三、試卷結構

四、題型示例1．單項選擇題（1）函數在上是A.單調增函數B.單調減函數C.上凸函數D.下凸函數（2）在高中數學教學中，課堂小結的方式多種多樣。有一種常見的小結方式是：結合板書內容梳理本課教學重點和難點的學習思路，同時提醒學生課下復習其中的要點。這種小結方式的作用在于A.升華情感，引起共鳴 B.點評議論，提高認識C.巧設懸念，激發興趣 D.總結回顧，強化記憶（3）在高等代數中，有一種線性變換叫做正交變換，即不改變任意兩點距離的變換。下列變換中不是正交變換的是A.平移變換 B.旋轉變換C.反射變換 D.相似變換2．簡答題（1）根據下圖編一道函數的應用問題（2）一位教師講了一堂公開課《函數

上一頁[1][2][3]下一頁

3．解答題已知0<，試證：4．論述題在必修模塊中，將平面解析幾何內容放在函數與立體幾何之后，對這種安排談談你的看法。5．案例分析題閱讀下列兩個對于不等式的教學活動設計，然后回答問題。設計1：活動（1）讓學生分別取a,b為具體數值，檢驗該不等式是否成立。活動（2）討論：，,的幾何意義。討論（1）：三個圖形的關系：討論（2）：該不等式何時等號成立，何時不等號成立？活動（3）不等式的嚴格證明討論（3）：若有三個數：a>0,b>0,c>0,是否會有一個什么相應的不等式？設計2：活動：學生分組討論不等式的證明方法。學生分組展示，討論。請回答如下問題：（1）分析設計1的教學設計意圖。（2）結合本案例分析合情推理與演繹推理的關系，簡述教學過程中如何引導學生經歷一個由合情推理到演繹推理的過程。（3）對比分析兩個教學設計的理念。6．教學設計題就高中數學“人教版教材”必修1第一單元中的函數概念第一課時的內容，設計一個教學方案（將提供教材內容）。

更多精彩資訊請關注查字典資訊網，我們將持續為您更新最新資訊!