解題關鍵:
1. 培養對數字計算的敏感度。
2. 熟練掌握各類基本數列(自然數列、平方數列、立方數列等)。
3. 熟練掌握所列的五大數列及其變形。
4. 掌握江蘇專有機械分組題型的練習。
數字推理題型一般包括以下幾個方面:
一。多級數列
【例1】9,20,42,86,( ),350
A.172 B.174 C.180 D.182
【答案】B
【解析】相鄰兩項兩兩相減,11,22,44,(88),(176),這是公比為2的等比數列。所以( )=86+88=174。因此,本題答案為B選項。
【例2】4,10,30,105,420,( )
A.956 B.1258 C.1684 D.1890
【答案】D
【解析】該數列相鄰兩項具有明顯的倍數關系,可采取兩兩做商,得到新數列:2.5,3,3,5,4,(4.5)所以( )=420*4.5=1890. 因此,本題答案為D選項。
【例3】82,98,102,118,62,138,( )
A. 68 B. 76 C. 78 D. 82
【答案】D
【解析】該數列相鄰兩項具有波動特性,可采取兩兩做和,得到新數列:180,200,220,180,200,(220)所以( )=220-138=82. 因此,本題答案為D選項。
二。 多重數列
【例1】1、3、2、6、5、15、14、( )、( )、 123
A.41,42 B.42,41 C.13,39 D.24,23
【答案】D
【解析】該數列項數過多,考慮奇偶項分開,奇數項:1,2,5,14,();偶數項:2,6,15,(),123,奇數與偶數項做差均為等比數列。 因此,本題答案為D選項。
【例2】1615,2422,3629,5436,( )
A.8150 B.8143 C.7850 D.7843
【答案】B此題考慮到每項的數字太大,可以把四位數分解成了2個兩位數,此數列就分解成:16,15,24,22,36,29,54,36,( )。考慮奇偶項分開,奇數項:16,24,36,54,();偶數項:15,22,29,36,()。奇數項是公比3/2的等比數列;偶數項為等差數列。
三。 冪次數列
【例1】36,125,256,243,64,( )
A.100 B.1 C.0.5 D.121
【答案】B
【解析】該數列中得每一項均具備完全的冪次變化形式,則可以將這次數字變化成冪次再找規律:62,53,44,35,26,(),則答案為17。
【例2】2,7,23,47,119( )
A: 125 B: 167 C: 168 D: 170
【答案】B
【解析】該數列中得每一項均具備完全的冪次變化的相關形式,則可以將這次數字變化成冪次再找規律:22-2,32-2,52-2,72-2,112-2,(),則答案為132-2=167。 四。 遞推數列
【例1】-3,10,7,17,( ),41
A.18 B.21 C.24 D.31
【答案】C
【解析】該數列中數字的整體變化規律為緩慢遞增,則在遞推數列中考慮加法:-3+10=7,10+7=17, 7+17=( 24 ),答案為C。
【例2】1,6,20,56,144,( ) 。
A.256 B.312 C.352 D.384
【答案】C
【解析】該數列中數字的整體變化規律為遞增偏快,考慮用倍數關系:12+4=6,6+8=20,202+16=56,562+32=144,1442+64=( 352)。
【例3】2、2、4、8、32、256、( )。
A.2048 B.4096 C.6942 D.8192
【答案】D
【解析】該數列中數字的整體變化規律為遞增非常快,考慮用乘法規律:22=4,2=8,48=32,832=256,32256=( 8192)。
【例4】2、3、7、45、2017、 ( ) 。
A.4068271 B.4068273 C.4068275 D.4068277
【答案】B
【解析】該數列中數字的整體變化規律為遞增劇快,考慮用平方關系:22-1=3,32-2=7,72-4=45,452-8=2107,21072-16=(4068273)。
五。 分數數列
【例1】2,11/3,28/5,53/7,86/9,( )
A.12 B.13 C.123/11 D.127/11
【答案】D
【解析】該數列是明顯的分數數列,考慮到分數中分母成明顯的等差數列,可以考慮這個數列的規律為分子分母各自成規律:分母是公差為2的等差數列,分子做一次差以后是公差為8的等差數列,答案為D。
【例2】2/3,1/3,5/12,2/15,53/480,( )
A.3/7 B.76/2568 C.652/27380 D.428/25440
【答案】D
【解析】把該數列反約分為:2/3,2/6,5/12,8/60,53/480,( ),可以觀察到分母是前項分數的分子與分母的乘積。因此()中分母是53.
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
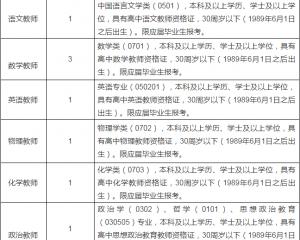 江西師范大學附屬中學2020年招聘教師2020-06-24
江西師范大學附屬中學2020年招聘教師2020-06-24 上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12 上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12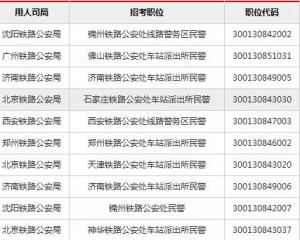 2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31
2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31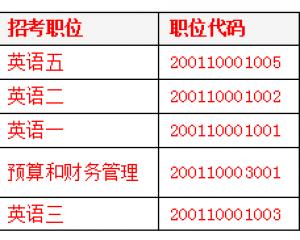 2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31
2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31