NewsContent"
山東公務員行測數字推理精選題及答案解析七十三
【721】 2,33,45,58,( )
A、49;B、59;C、64;D、612
解析:選D,把數列中的各數的十位和個位拆分開=>可以分解成3、4、5、6與2、3、5、8、12 的組合。3、4、5、6 一級等差,2、3、5、8、12 二級等差
【722】 2,2,0,7,9,9,( )
A.13;B.12;C.18;D.17
解析:2+2+0=4; 2+0+7=9; 0+7+9=16;7+9+9=25;9+9+?=36; ?=18
【723】 3,2,5/3,3/2,( )
A.7/5;B.5/6;C.3/5;D.3/4
解析:(方法一)3/1、2/1、5/3、3/2、7/5=>分子減分母=>2、1、2、1、2 =>答案A(方法二)原數列3,2,5/3,3/2 可以變為3/1,4/2,5/3,6/4,分子上是3,4,5,6,分母上是1,2,3,4,均夠成自然數數列,由此可知下一數為7/5
【724】 95,88,71,61,50,( )
A.40; B.39;C.38;D.37
解析:95 - 9 - 5 = 81; 88 - 8 - 8 = 72; 71 - 7 - 1 = 63;61 - 6 - 1 = 54; 50 - 5 - 0 = 45; 40 - 4 - 0 = 36 ; 所以選 A、40 。
【725】 32,98,34,0,( )
A.1;B.57; C.3; D.5219
解析:思路:這類題每兩數字項之間的差值相差很大,而且又沒有什么聯系,答案的數字相差也很大,雜看是很亂沒什么規律。這時我們不防拋去傳統的思路,就從每個數字項直接下手,考慮怎么把這數列轉成新的數列(注:個人認為考慮如何成為新的數列應該以每一項數字的本意去推,如:只有一位數字的數字項2,我們不能推為0-2或0×2,因為這樣推出答案不具備唯一性,往往會讓你陷入誤區。),再找出彼此之間的規律!32=>2-3=-1(即后一數減前一個數),98=>8-9=-1,34=>4-3=1,0=>0(因為0這一項本身只有一個數字,故還是推為0),?=>?得新數列:-1,-1,1,0,?;再兩兩相加再得出一個新數列:-2,0,1.?;2×0-2=-2;2×1-2=0;2×2-3=1;2×3-3=3
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
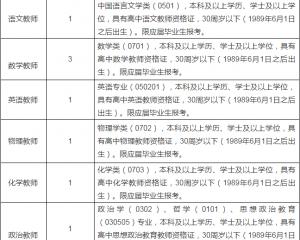 江西師范大學附屬中學2020年招聘教師2020-06-24
江西師范大學附屬中學2020年招聘教師2020-06-24 上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12 上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12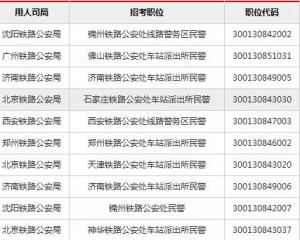 2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31
2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31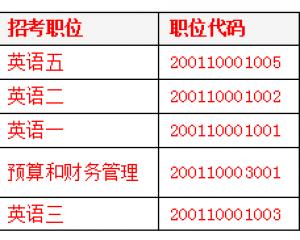 2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31
2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31