NewsContent"
數學運算上
(注意運算不要算錯,看錯!!!越簡單的題,越要小心陷阱) 一.排列組合問題 1.能不用排列組合盡量不用。用分步分類,避免錯誤 2.分類處理方法,排除法。 例:要從三男兩女中安排兩人周日值班,至少有一名女職員參加,有(C1/2 *C1/3 +1)種不同的排法? 析:當只有一名女職員參加時,C1/2* C1/3; 當有兩名女職員參加時,有1種 3.特殊位置先排 例:某單位安排五位工作人員在星期一至星期五值班,每人一天且不重復。若甲乙兩人都不能安排星期五值班,則不同的排班方法共有(3 * P4/4) 析:先安排星期五,后其它。 4. 相同元素的分配(如名額等,每個組至少一個),隔板法。 例:把12個小球放到編號不同的8個盒子里,每個盒子里至少有一個小球,共有(C7/11)種方法。 析:0 0 0 0 0 0 0 0 0 0 0 0 ,共有12-1個空,用8-1個隔板插入,一種插板方法對應一種分配方案,共有C7/11種,即所求。 注意:如果小球也有編號,則不能用隔板法。 5. 相離問題(互不相鄰)用插空法 例:7人排成一排,甲、乙、丙3人互不相鄰,有多少種排法? 析: 0 0 0 0 ,分兩步。第一步,排其它四個人的位置,四個0代表其它四個人的位置,有P4/4種。第二步,甲乙丙只能分別出現在不同的 上,有P3/5種,則P4/4 * P3/5即所求。 例:在一張節目表中原有8個節目,若保持原有的相對順序不變,再增加三個節目,求共有多少種安排方法? 析:思路一,用二次插空法。先放置8個節目,有9個空位,先插一個節目有9種方法,現在有10個空位,再插一個節目有10種方法,現有11種空位,再插一種為11種方法。則共有方法9*10*11。 思路二,可以這么考慮,在11個節目中把三個節目排定后,剩下的8個位置就不用排了,因為8個位置是固定的。因此共有方法P3/11 6. 相鄰問題用捆綁法 例:7人排成一排,甲、乙、丙3人必須相鄰,有多少種排法? 析:把甲、乙、丙看作整體X。第一步,其它四個元素和X元素組成的數列,排列有P5/5種;第二步,再排X元素,有P3/3種。則排法是P5/5 * P3/3種。 7. 定序問題用除法 例:有1、2、3,...,9九個數字,可組成多少個沒有重復數字,且百位數字大于十位數字,十位數字大于個位數字的5位數? 析:思路一:1-9,組成5位數有P5/9。假設后三位元素是(A和B和C,不分次序,ABC任取)時(其中B>C>A),則這三位是排定的。假設B、C、A這個順序,五位數有X種排法,那么其它的P3/3-1個順序,都有X種排法。則X*(P3/3-1+1)=P5/9,即X=P5/9 / P3/3 思路二:分步。第一步,選前兩位,有P2/9種可能性。第二步,選后三位。因為后三位只要數字選定,就只有一種排序,選定方式有C3/7種。即后三位有C3/7種可能性。則答案為P2/9 * C3/7 8. 平均分組 例:有6本不同的書,分給甲、乙、丙三人,每人兩本。有多少種不同的分法? 析:分三步,先從6本書中取2本給一個人,再從剩下的4本中取2本給另一個人,剩下的2本給最后一人,共C2/6* C2/4 * C2/2 例:有6本不同的書,分成三份,每份兩本。有多少種不同的分法? 析:分成三份,不區分順序,是無序的,即方案(AB,CD,EF)和方案(AB,EF,CD)等是一樣的。前面的在(C2/6* C2/4 * C2/2)個方案中,每一種分法,其重復的次數有P3/3種。則分法有,(C2/6* C2/4 * C2/2) / P3/3 種分法。 二.日期問題 1.閏年,2月是29天。平年,28天。
判定公歷閏年遵循的一般規律為: 四年一閏,百年不閏,四百年再閏.
公歷閏年的精確計算方法:(按一回歸年365天5小時48分45.5秒)
①、普通年能被4整除而不能被100整除的為閏年。(如2004年就是閏年,1900年不是閏年)
②、世紀年能被400整除而不能被3200整除的為閏年。(如2000年是閏年,3200年不是閏年)
③、對于數值很大的年份能整除3200,但同時又能整除172800則又是閏年.(如172800年是閏年,86400年不是閏年)
公元前閏年規則如下:
1,非整百年:年數除4余數為1是閏年,即公元前1、5、9……年;
2,整百年:年數除400余數為1是閏年,年數除3200余數為1,不是閏年,年數除172800余1又為閏年,即公元前401、801……年。
NewsContent" 2.口訣: 平年加1,閏年加2;(由平年365天/7=52余1得出)。 例:2002年 9月1號是星期日 2008年9月1號是星期幾? 因為從2002到2008一共有6年,其中有4個平年,2個閏年,求星期,則: 4X1+2X2=8,此即在星期日的基礎上加8,即加1,第二天。 例:2004年2月28日是星期六,那么2008年2月28日是星期幾? 4+1=5,即是過5天,為星期四。(08年2 月29日沒到)(似乎錯了2004也是閏年)三.集合問題 1.兩交集通解公式(有兩項) 公式為:滿足條件一的個數+滿足條件二的個數-兩者都滿足的個數=總個數-兩者都不滿足的個數。即:A+B=A∪B-A∩B
其中滿足條件一的個數是指 只滿足條件一不滿足條件二的個數 加上 兩條件都滿足的個數 公式可以畫圖得出 例:有62名學生,會擊劍的有11人,會游泳的有56人,兩種都不會用的有4人,問兩種都會的學生有多少人? 思路一:兩種都會+只會擊劍不會游泳+只會游泳不會擊劍=62-4 設都會的為T,11-T+56-T+T=58,求得T=9 思路二:套公式,11+56-T=62-4,求得T=9 例:對某小區432戶居民調查汽車與摩托車的擁有情況,其中有汽車的共27戶,有摩托車的共108戶,兩種都沒有的共305戶,那么既有汽車又有摩托車的有多少戶? 析:套用公式27+108-T=432-305 得T=8 2.三交集公式(有三項)
A+B+C=A∪B∪C+A∩B+B∩C+A∩C-A∩B∩C
例:學校教導處對100名同學進行調查,結果有58人喜歡看球賽,有38人喜歡看戲劇,有52人喜歡看電影。另外還知道,既喜歡看球賽又喜歡看戲劇(但不喜歡看電影)的有6人,既喜歡看電影又喜歡看戲劇(但不喜歡看球賽)的有4人,三種都喜歡的有12人,則只喜歡看電影的人有多少人?
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
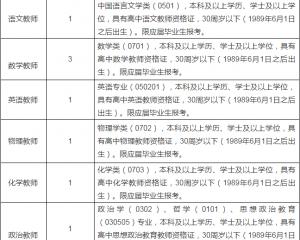 江西師范大學附屬中學2020年招聘教師2020-06-24
江西師范大學附屬中學2020年招聘教師2020-06-24 上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12 上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12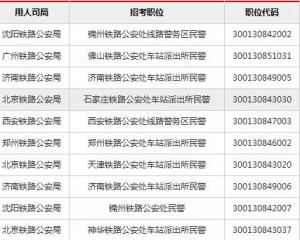 2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31
2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31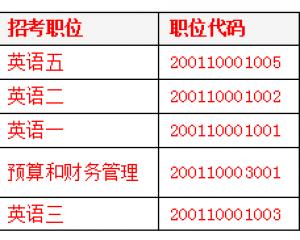 2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31
2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31