在做數學題時,常常運用邏輯推理方法,一步一步地尋求必要條件,最后求得結論,這是一種常用的方法。對于有些問題,若能根據其具體情況,合理地、巧妙地對某些元素賦值,特別是賦予確定的特殊值,往往能使問題獲得簡捷有效的解決。在公務員行測考試的工程問題中,賦值法有著非常廣泛的應用,很多考生卻不清楚到底什么時候應用該種方法,以及在賦值的時候到底把哪個量設為特值。下面就重點介紹工程問題中賦值法的應用。
工程問題的核心公式:工作總量=工作效率×工作時間。其中一共含有三個量,如果這三個量只給出了一個,那么就需要對另外兩個量中的一個進行賦值,只有這樣,上述這個公式才能夠計算。在工程問題中,一般給工作總量或者工作效率進行賦值。另外,在賦值的時候盡量賦最小公倍數,避免出現分數的情況,減小計算量。
一、設工作總量
【例1】一批紅棗,甲單獨運出需要8天,乙單獨運出需要6天,甲乙合作3天后,還余下3噸沒有運,問:這批紅棗共有多少噸?
【解析】此時應設工作總量為8和6的最小公倍數24,那么甲、乙的工作效率分別是3和4,甲乙3天共完成3×(3+4)=21,剩余3,對應是剩余3噸,說明一份對應一噸,原工作總量為24份,共計24噸。
【例2】一項工程,甲一人做完需30天,甲、乙合作完成需18天,乙、丙合作完成需15天,甲、乙、丙三人共同完成該工程需:( )
A.10天 B.12天
C.8天 D.9天
【解析】A。由于要求甲、乙、丙三人共同完成該工程,所以只要求出三人的工作效率就可以。根據題意,甲需要30天,乙、丙合作需要15天,這兩個條件就可求出三人的效率。因此可對工作總量賦值為30,那么甲的效率為1,乙、丙兩人的效率為2,所以三人的總效率為1+2=3,甲、乙、丙三人共需要10天完成該工程。
小結:當題干中含有完成整個工程所需時間T時,可以設工程量為T的倍數。
二、設工作效率
【例3】早上7點兩組農民開始在麥田里收割麥子,其中甲組20人,乙組15人。8點半,甲組分出10人捆麥子;10點,甲組將本組所有已割的麥子捆好后,全部幫乙組捆麥子;如果乙組農民一直在割麥子,什么時候乙組所有已割的麥子能夠捆好?(假設每個農民的工作效率相同)
A.10:45 B.11:00
C.11:15 D.11:30
【解析】B。由題意知捆麥子的效率要大于收割麥子的效率,由于每個農民的工作效率相同,所以就可以設每個農民每小時收割麥子的效率為1,甲組中有10個農民割麥子3小時,10個農民割麥子1.5小時,工作量為10×3+10×1.5=45,10個農民用1.5小時將其捆完,每個農民每小時捆麥子的效率為45÷1.5÷10=3。假如甲組農民用了t時刻將乙組農民收割的麥子捆完,那么乙組農民收割麥子的時間為(t+3),收割總量為15×(t+3),甲組農民所捆乙組的麥子量=甲組農民捆麥子的效率×20×t=3×20×t,則15×(t+3)=3×20×t,解得t=1,也就是用了1小時甲組農民將乙組所有已割的麥子能夠捆好,此時為10+1=11點。
當題干中已知有兩個或以上的工程量時,此時就可以對工作效率進行賦值,求出相應的工作總量,然后再進行解題。
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
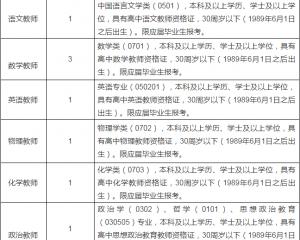 江西師范大學附屬中學2020年招聘教師2020-06-24
江西師范大學附屬中學2020年招聘教師2020-06-24 上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12 上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12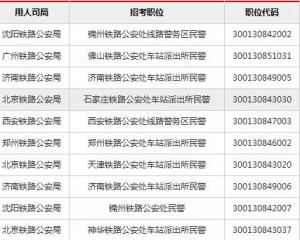 2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31
2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31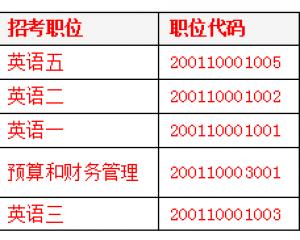 2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31
2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31