按照常考的題型,余數問題可以分為以下幾類: 代入排除類型、余數關系式和恒等式的應用、同余問題、同余問題的延伸。
一、代入排除類型
例1:學生在操場上列隊做操,只知人數在90-110之間。如果排成3排則不多不少;排成5排則少2人;排成7排則少4人;則學生人數是多少?( )
A.102 B.98 C.104 D.108
【解析】對于余數問題我們可以優先考慮代入排除法。直接代入選項,看看哪個符合題目所給的條件,選項108滿足條件,因此選擇D選項。
例2:在一個除法算式里,被除數、除數、商和余數之和是319,已知商是21,余數是6,問被除數是多少?( )
A.237 B.258 C.279 D.290
【解析】對于余數問題我們可以優先考慮代入排除法。根據題目可得被除數+除數=319-21-6=292。直接代入選項,如代入A項,可得除數為292-237=55,利用被除數=除數乘以商再加余數,這個等式利用尾數法,來快速排除答案。最后可得選擇C選項。
二、余數關系式和恒等式的應用
余數的關系式和恒等式比較簡單,因為這一部分的知識點在小學時候就已經學過了,余數基本關系式:被除數÷除數=商…余數(0≤余數<除數),但是在這里需要強調兩點:
1、余數是有范圍的(0≤余數<除數),這需要引起大家足夠的重視,因為這是某些題目的突破口。
2、由關系式轉變的余數基本恒等式需要掌握:被除數=除數×商+余數。
例3:兩個整數相除,商是5,余數是11,被除數、除數、商及余數的和是99,求被除數是多少?( )
A.12 B.41 C.67 D.71
【解析】余數是11,因此,根據余數的范圍(0≤余數<除數),我們能夠確定除數>11。除數為整數,所以除數≥12,根據余數的基本恒等式:被除數=除數×商+余數≥12×商+余數=12×5+11=71,因此被除數最小為71,答案選擇D選項。
例4:有四個自然數A、B、C、D,它們的和不超過400,并且A除以B商是5余5,A除以C商是6余6,A除以D商是7余7。那么,這四個自然數的和是?()
A.216 B.108 C.314 D.348
【解析】利用余數基本恒等式:被除數=除數×商+余數,有A=B×5+5= (B+1)×5。由于A、B均是自然數,于是A可以被5整除,同理,A還可以被6、7整除,因此,A可以表示為5、6、7的公倍數,即210n。由于A、B、C、D的和不超過400,所以A只能等于210,從而可以求出B=41、C=34、D=29,得到A+B+C+D=314,選C。
【小結】像上面這兩個題目,就是活用這兩個知識點來解題的,所以在對這類問題的練習過程中,一定要牢牢地把握這兩點,我們就可以快速的解題。
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
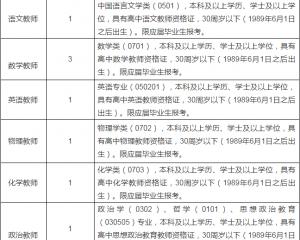 江西師范大學附屬中學2020年招聘教師2020-06-24
江西師范大學附屬中學2020年招聘教師2020-06-24 上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12 上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12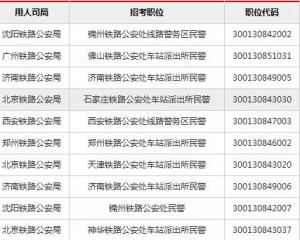 2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31
2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31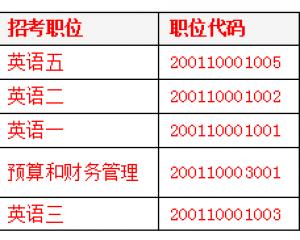 2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31
2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31